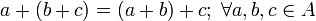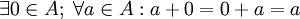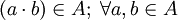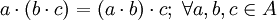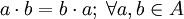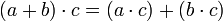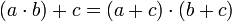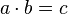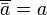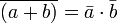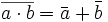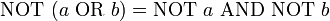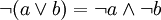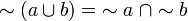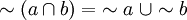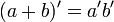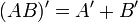miércoles, 24 de diciembre de 2008
CONTADORES
Clasificación de los contadores [editar]
Según la forma en que conmutan los biestables, podemos hablar de contadores síncronos (todos los biestables conmutan a la vez, con una señal de reloj común) o asíncronos (el reloj no es común y los biestables conmutan uno tras otro).
Según el sentido de la cuenta, se distinguen en ascendentes, descendentes y UP-DOWN (ascendentes o descendentes según la señal de control).
Según la cantidad de números que pueden contar, se puede hablar de contadores binarios de n bits (cuentan todos los números posibles de n bits, desde 0 hasta 2n − 1), contadores BCD (cuentan del 0 al 9) y contadores Módulo N (cuentan desde el 0 hasta el N-1)
Tipos de contadores [editar]
Existen diversos tipos de contadores:
Contadores de rizado.
Contadores paralelos.
Contadores de rizado mod-6.
Contador Johnson. Activa una sola salida entre varias. En respuesta al pulso de conteo, la salida siguiente pasa a ser la activa. No se emplea un contador binario seguido de un decodificador debido a que, al conmutar entre dos estados, podría producir pulsos espúreos en otras salidas. El 4017 es un contador johnson de 10 estados.
Contador en anillo. Está formado por un conjunto de biestables conectados como un registro de desplazamiento, con un lazo de realimentación que se obtiene uniendo las salidas del último biestable con la entrada del primero. El inconveniente que presentan es que sólo pueden contar 'n' impulsos (siendo log2m y m los bits del resultado).
“Se utilizan para llevar el control del número de ocasiones en que se realiza una operación o se cumple una condición. Los incrementos son generalmente de uno en uno.”
FLIP FLOP
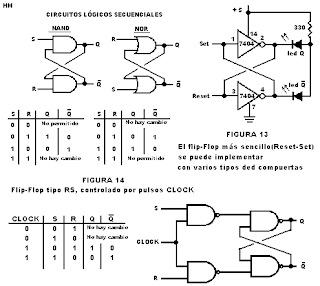
Asíncronos: sólo tienen entradas de control. El más empleado es el biestable RS.
Síncronos: además de las entradas de control posee una entrada de sincronismo o de reloj. Si las entradas de control dependen de la de sincronismo se denominan síncronas y en caso contrario asíncronas. Por lo general, las entradas de control asíncronas prevalecen sobre las síncronas.
La entrada de sincronismo puede ser activada por nivel (alto o bajo) o por flanco (de subida o de bajada). Dentro de los biestables síncronos activados por nivel están los tipos RS y D, y dentro de los activos por flancos los tipos JK, T y D.
R: el borrado (reset en inglés), puesta a 0 ó nivel bajo de la salida.
S: el grabado (set en inglés), puesta a 1 ó nivel alto de la salida.
Si no se activa ninguna de las entradas, el biestable permanece en el estado que poseía tras la última operación de borrado o grabado. En ningún caso deberían activarse ambas entradas a la vez, ya que esto provoca que las salidas directa (Q) y negada (Q') queden con el mismo valor: a bajo, si la báscula está construida con puertas NO-O (NOR), o a alto, si con puertas NO-Y (NAND). El problema de que ambas salidas queden al mismo estado está en que al desactivar ambas entradas no se podrá determinar el estado en el que quedaría la salida. Por eso, en las tablas de verdad, la activación de ambas entradas se contempla como caso no deseado (N. D.).
LATCH
 upan en múltiples, algunos de los cuales tienen nombres especiales, como por ejemplo el 'latch quad ' (que puede almacenar cuatro bits) y el 'latch octal' (ocho bits). Los latches son dispositivos biestables que no tienen entrada de reloj y cambian el estado de salida solo en respuesta a datos de entrada, mientras que los flip-flops cuando tienen data de entrada cambian el estado de salida en respuesta a una entrada de reloj.
upan en múltiples, algunos de los cuales tienen nombres especiales, como por ejemplo el 'latch quad ' (que puede almacenar cuatro bits) y el 'latch octal' (ocho bits). Los latches son dispositivos biestables que no tienen entrada de reloj y cambian el estado de salida solo en respuesta a datos de entrada, mientras que los flip-flops cuando tienen data de entrada cambian el estado de salida en respuesta a una entrada de reloj.DESCODICADORES

Este dispositivo tiene varias salidas, y se activará aquella que establezca el código aplicado a la entrada.
Con un código de n bits se pueden encontrar 2n posibles combinaciones. Si se tienen 3 bits (3 entradas) serán posibles 23 = 8 combinaciones.
Una combinación en particular activará sólo una salida.
CODIFICADORES

Existen dos tipos fundamentales de codificadores: codificadores sin prioridad y codificadores con prioridad. En el caso de codificadores sin prioridad, puede darse el caso de salidas cuya entrada no pueda ser conocida: por ejemplo, la salida 0 podría indicar que no hay ninguna entrada activada o que se ha activado la entrada número 0. Además, ciertas entradas pueden hacer que en la salida se presente la suma lógica de dichas entradas, ocasionando mayor confusión. Por ello, este tipo de codificadores es usado únicamente cuando el rango de datos de entrada está correctamente acotado y su funcionamiento garantizado.
martes, 23 de diciembre de 2008
teorema de morgan
(X + Y)´ = X´ Y´
(XY)´ = X´ + Y´
MAPAS KARNAUGH
Una vez hecho el mapa, debemos marcar las regiones contiguas que manejen 1s. Aquí en el dibujo vemos cómo se marcan dos regiones. Estas regiones son las simplificaciones. Como la región azul involucra solamente a la b, eso representa. La región verde, por su parte, involucra solamente a la a. Para cada región, debemos checar qué variables involucra. En el caso de la región azul, cubre a la b, pero con respecto a la variable a maneja tanto a como a', y por eso se descarta la a. Una vez definidas las regiones, se escribe la función simplificada f= b + a.
Ejemplo 2: Simplifica la función de tres variables f = a'b + ab'c + c'Lo primero que debo de hacer es representarlo en un mapa de tres variables. Se representa como se muestra en la tabla. Para llenar la tabla, pongo un uno donde se intersecte el valor de la función. Por ejemplo, para los términos de la función f = a'b +ab'c + c', se ha marcado donde se puso el 1 en la tabla.
debemos buscar las regiones que nos indiquen la función simplificada. Lo primero que debemos observar es que las regiones pueden agruparse de los extremos del mapa, como la región azul.
Esta región representa a c'. Ahora, vemos que queda un bit en a'bc, pero siempre conviene agruparlo lo más posible, en regiones cuyas celdas sean múltiplos de 2 (1, 2, 4, 8...) En este caso, la agrupamos con el 1 contiguo, para que la región quede como a'b.La región verde se agrupa para formar ab'. Así, la función resultante sería f = a'b + ab' + c.
Ejemplo 3: Simplifica la función de cuatro variables f = ac'd' + a'bd + abcd + ab'cd + a'bc'd' + a'b'c'd'Nuevamente, lo primero que hacemos es vaciar la función al mapa. Nótese la forma que toma el mapa. Ahora, lo siguiente es agrupar las variables en regiones. La primer a región, la roja, está agrupada de las esquinas. Esta agrupación representa a c'. La siguiente región, la verde la agrupo con el 1 que tiene abajo. Pude haberla agrupado con el 1 a la derecha, pero hubiera significado agrupar un 1 ya agrupado, y dejar otro 1 aún no agrupado sin agrupar. Así que se agrupa de esta forma, y la región verde representa a a'bd. Los 1s que quedan hasta este momento libre pueden agruparse juntos, en la región azul. Esto representa a acd.
Es importante notar la región naranja. Representa a bcd. Esta región es una simplificación adicional válida, que pudo haberse manejado. En ocasiones, habrá varias formas de agrupar a los 1s. Todas son válidas, y representan soluciones equivalentes. Sin embargo, hay que cuidar de siempre agrupar las regiones lo más grandes posibles, y cuidando de agrupar a los 1s de manera que se repitan lo menos posible.
MÉTODO DE REDUCCIÓN DE MAPAS DE KARNAUGH
El Álgebra de Boole, resuelve problemas que dependiendo del número de términos que tenía la función canónica, siendo el número de compuertas lógicas utilizadas igual al número de términos obtenidos MÁS UNO; por lo tanto, los circuitos obtenidos son de dos niveles de conmutación con un tiempo mínimo de retardo, pero que de ninguna manera es el más sencillo ni el más económico.
2.1 Generación de MAPA DE KARNAUGH de 2 y 3 variables.
Los mapas de Karnaugh es uno de los métodos más prácticos. Se puede decir que es el más poderoso, cuando el número de variables de entrada es menor o igual a seis; más allá, ya no es tan práctico. En general, el mapa de Karnaugh se considera como la forma gráfica de una tabla de verdad o como una extensión del diagrama de Venn.
Antes de explicar como se utiliza el mapa de Karnaugh en la minimización de funciones, veremos como se obtiene el mapa. Esto nace de la representación geométrica de los números binarios. Un número binario de n bits, puede representarse por lo que se denomina un punto en un espacio N. Para entender lo que se quiere decir con esto, considérese el conjunto de los números binarios de un bit, es decir 0 o 1. Este conjunto puede representarse por dos puntos en un espacio 1; esto es, por dos puntos unidos por una línea. Tal representación se denomina un cubo 1.
algebra booleana
Definición [editar]
El Álgebra de Boole es una estructura algebraica que puede ser considerada desde distintos puntos de vista matemáticos:
Como retículo [editar]
El álgebra de Boole es un retículo (A,  , +), donde el conjunto A esta formado por dos elementos A={0, 1}, como retículo presenta las siguientes propiedades:
, +), donde el conjunto A esta formado por dos elementos A={0, 1}, como retículo presenta las siguientes propiedades:
1. Ley de Idempotencia:
2. Ley de Asociatividad:
3. Ley de Conmutatividad:
4. Ley de Cancelativo
Como anillo [editar]
El Álgebra de Boole tiene Estructura algebraica de Anillo:
Grupo abeliano respecto a (+) [editar]
El conjunto A={0,1} es un Grupo abeliano respecto a (+):
1. (+) es una operación interna en A:
2. Es asociativa:
3. Tiene elemento neutro
4. Tiene elemento simétrico:
5. es conmutativa:
Grupo abeliano respecto a (·) [editar]
El conjunto A={0,1} es un Grupo abeliano respecto a ( ):
):
6. ( ) es una operación interna en A:
) es una operación interna en A:
7. Es asociativa:
8. Tiene elemento neutro
9. Tiene elemento simétrico:
10. es conmutativa:
Distributivo [editar]
El conjunto A={0,1} es un Grupo abeliano respecto a (+) y ( ) y es distributiva:
) y es distributiva:
11. La operación (+) es distributiva respecto a ( ):
):
12. La operación ( ) es distributiva respecto a (+):
) es distributiva respecto a (+):
Como resultado podemos decir que el Álgebra de Boole tiene Estructura algebraica de anillo conmutativo y con elemento neutro respecto a las dos operaciones (+) y ( ).
).
Operaciones [editar]
Hemos definido el conjunto A = {0,1} como el conjunto universal sobre el que se aplica el álgebra de Boole, sobre estos elementos se definen varias operaciones, veamos las más fundamentales:
Operación suma [editar]
| a | b | a + b |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
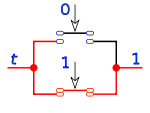
La operación suma (+) asigna a cada par de valores a, b de A un valor c de A:
Su equivalencia en lógica de interruptores es un circuito de dos interruptores en paralelo.
Si uno de los valores de a o b es 1, el resultado será 1, es necesario que los dos sumandos sean 0, para que el resultado sea 0.
 |  |  |  |
Operación producto [editar]
| a | b | a  b b |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
La operación producto ( ) asigna a cada par de valores a, b de A un valor c de A:
) asigna a cada par de valores a, b de A un valor c de A:
Esta operación en lógica de interruptores es un circuito en serie de dos interruptores
solo si los dos valores a y b son 1, el resultado será 1, si uno solo de ellos es 0 el resultado será 0.
 |  |  |  |
Operación negación [editar]
| a | 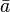 |
| 0 | 1 |
| 1 | 0 |
La operación negación presenta el opuesto del valor de a:
Un interruptor inverso equivale a esta operación:
 |  |
Operaciones combinadas [editar]
| a | b | 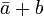 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Partiendo de estas tres operaciones elementales se pueden realizar otras más complejas, que podemos representar como ecuaciones booleanas, por ejemplo:
Que representado en lógica de interruptores es un circuito de dos interruptores en paralelo, siendo el primero de ellos inverso.
La distinta secuencia de valores de a y b da los resultados vistos en la tabla de verdad.
 |  |  |  |
Leyes fundamentales [editar]
El resultado de aplicar cualquiera de las tres operaciones definidas a variables del sistema booleano resulta en otra variable del sistema, y este resultado es único.
1. Ley de idempotencia:
2. Ley de involución:
3. Ley conmutativa:
4. Ley asociativa:
5. Ley distributiva:
6. Ley de cancelación:
Principio de dualidad [editar]
El concepto de dualidad permite formalizar este hecho: a toda relación o ley lógica le corresponderá su dual, formada mediante el intercambio de los operadores unión (suma lógica) con los de intersección (producto lógico), y de los 1 con los 0.
Además hay que cambiar cada variable por su negada. Esto causa confusión al aplicarlo en los teoremas básicos, pero es totalmente necesario para la correcta aplicación del principio de dualidad. Véase que esto no modifica la tabla adjunta.
-
Adición Producto 1 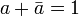

2 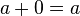
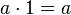
3 

4 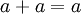

5 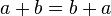
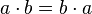
6 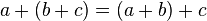
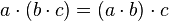
7 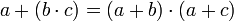
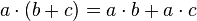
8 
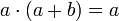
9 
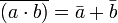
Otras formas de notación del álgebra de Boole [editar]
En matemática se emplea la notación empleada hasta ahora ({0,1}, + ,  ) siendo la forma más usual y la más cómoda de representar.
) siendo la forma más usual y la más cómoda de representar.
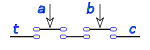
Por ejemplo las leyes de De Morgan se representan así:
Cuando el álgebra de Boole se emplea en electrónica, suele emplearse la misma denominación que para las puerta lógica AND (Y), OR (O) y NOT (NO), ampliándose en ocasiones con X-OR (O exclusiva) y su negadas NAND (NO Y), NOR (NO O) y X-NOR (equivalencia). las variables pueden representarse con letras mayúsculas o minúsculas, y pueden tomar los valores {0, 1}
Empleando esta notación las leyes de De Morgan se representan:
En su aplicación a la lógica se emplea la notación 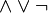 y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}
y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}
Con la notación lógica las leyes de De Morgan serian así:
En el formato de Teoría de conjuntos el Álgebra de Boole toma el aspecto: 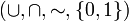
En esta notación las leyes de De Morgan serian así:
Desde el punto de vista practico existe una forma simplificada de representar expresiones booleanas. Se emplean apóstrofes (') para indicar la negación, la operación suma (+) se representa de la forma normal en álgebra, y para el producto no se emplea ningún signo, las variables se representan, normalmente con una letra mayúscula, la sucesión de dos variables indica el producto entre ellas, no una variable nombrada con dos letras.
La representación de las leyes de De Morgan con este sistema quedaría así, con letra minúsculas para las variables:
y así, empleando letras mayúsculas para representar las variables:
Todas estas formas de representación son correctas, se utilizan de hecho, y pueden verse al consultar bibliografía. La utilización de una u otra notación no modifica el álgebra de Boole, solo su aspecto, y depende de la rama de las matemáticas o la tecnología en la que se este utilizando para emplear una u otra notación.